ОПТИМАЛЬНЫЙ РАСКРОЙ ТКАНИ

Задача оптимального раскроя куска материи на выкройки заданной формы существует давно. Оптимальность означает минимизацию отходов материи при соблюдении заданной пропорции в количестве выкроек разного фасона.

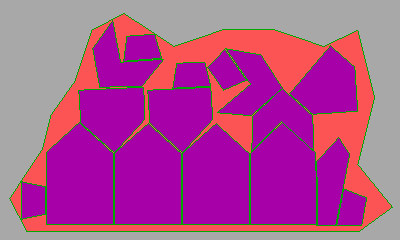Чаще всего задача решается стандартными математическими методами оптимизации. Однако, в данном случае стандартные методы использовать было невозможно, поскольку и исходный кусок ткани, и (тем более) требуемые выкройки имели форму не прямоугольную, а произвольную, с округлыми сторонами. Исходя из этого, был выбран эвристический метод, не имеющий конкретной математической основы. Метод полностью создан автором данной программы. Разумеется, для некоторого упрощения все округлые формы были заменены ломаными линиями. Это не привело к большой погрешности в расчетах, но зато существенно упростило алгоритмизацию.

Программа разрабатывалась на первых персональных компьютерах с частотой не больше 8МГц (в 300 раз меньше, чем сейчас), первые версии работали по несколько часов. Разумеется, это не позволяло сделать программу очень сложной, но зато это дало стимул искать эффективные алгоритмы оптимизации. В результате время расчетов сократилось до 10-40 минут. На современных компьютерах время расчетов фактически пренебрежимо мало.

К сожалению, работа над программой не была доведена до полного завершения. Автору пришлось также самому писать блок вывода информации (хотя изначально этим должны были заниматься другие), что отвлекло его от основной работы. Правда, при написании вывода были решены интересные практические задачи построения произвольных фигур. Нужно учитывать, что программа была написана в среде МС-ДОС при полном отсутствии каких-либо графических библиотек.

В данное время программа существует в первозданном виде 20-летней давности, но при необходимости (наличие конкретного заказа) она может быть возрождена и усовершенствована в соответствии с нынешними техническими возможностями. На этой странице приведен один пример раскроя.